keyposture.

75% of musicians experience playing related injuries that hinder their ability to play instruments. A solution was devised that optimizes and monitors a pianist’s movements, providing feedback in regards to proper posture and suggesting appropriate rest times in order to prevent the development of bad habits that lead to injury. This page provides a brief overview of the engineering analysis undertaken and the designed solution.

Members: Ali Vira, Adrienne Chan, Charis Chao, Evan Shen

Engineering Analysis

Functional, user, and engineering requirements were created. A mathematical model was created to isolate moments at the joints in a pianist’s arm. MATLAB was used to optimize the model and run sensitivity analyses. The designed solution features two main components, a tracking component to identify and optimize posture, and a feedback component to inform the pianist how they are playing. The development of the solution followed an iterative design process. A Kinect and a connected web application were ultimately respectively selected as the two main design components. Functional tests were performed on the hardware and software components. The software was further tested for speed and accuracy. User tests were conducted on experienced piano players.

Requirements

Interviews with piano teachers, pianists, professors, and researchers were combined with research gleaned from state of the art products and academic papers to generate the following requirements.

Functional

Measure...

Angle of wrists, elbows, and shoulder

Calculate and inform user of...

Safety level
Appropriate time to take a break

Record and replay audio
Provide visual cues of safety level

User

Cannot interfere with playing
Aesthetically pleasing
Provide feedback in a meaningful manner

Engineering

Wearable weight < 100g if applicable
Cost < $150
Error tolerance - Must capture movement within 4cm

Mathematical model

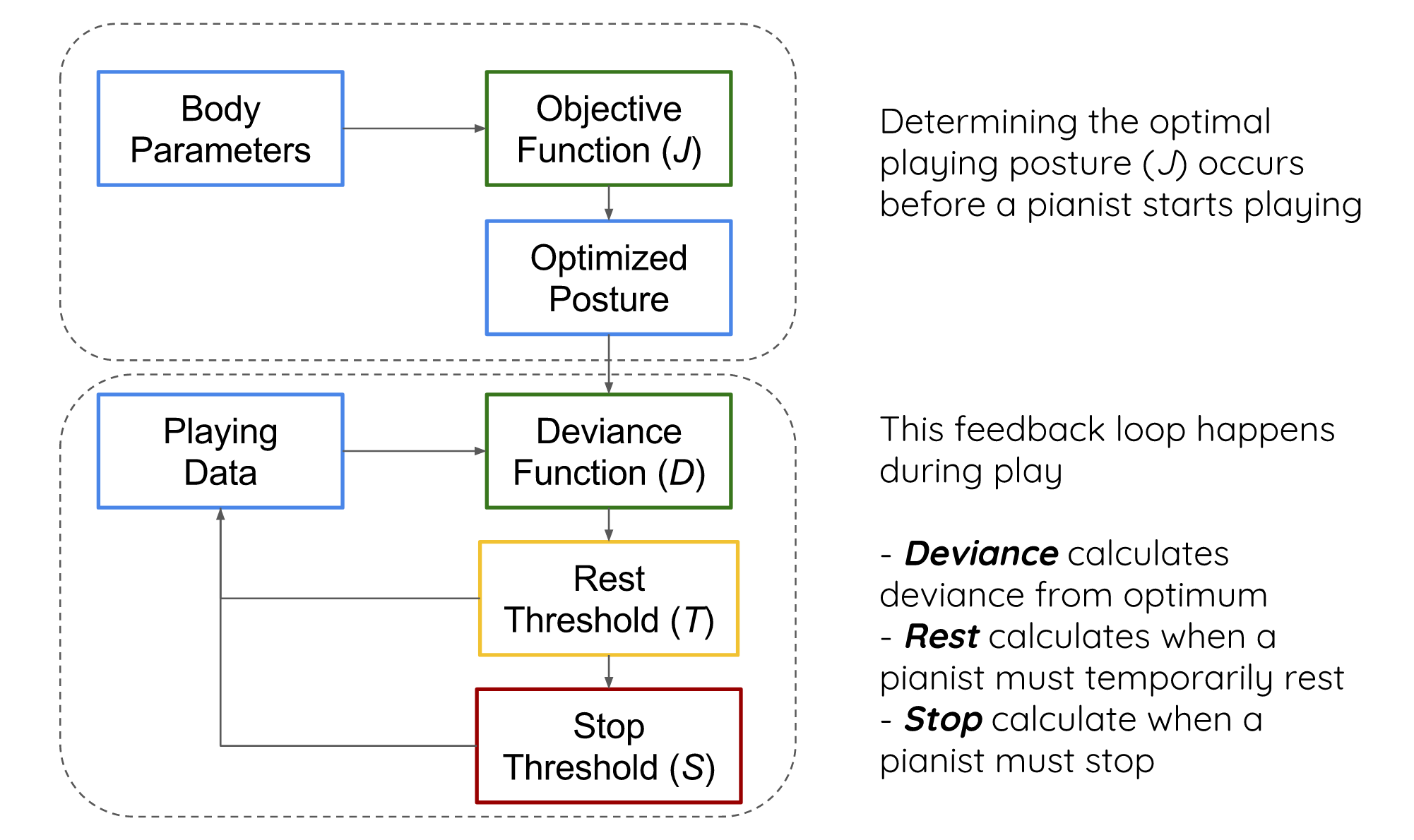
The mathematical model was divided into two main components. The first half of model optimized a pianist’s playing position. The second part of the model monitored the pianist’s playing position to identify posture deviances from the optimum posture, inform the pianist when a rest was needed, and inform the pianist when to stop playing entirely. Figure 1 below provides a graphical illustration of the mathematical model.

Optimization

The optimization model was designed to minimize the moments experienced by a pianist at the wrist, elbow, and shoulder joints. A planar, static, linked segment model of the human arm was created. The position of the back was fixed to constrain the number of equations in the optimization problem such that the problem could be inputted into a MATLAB solver.

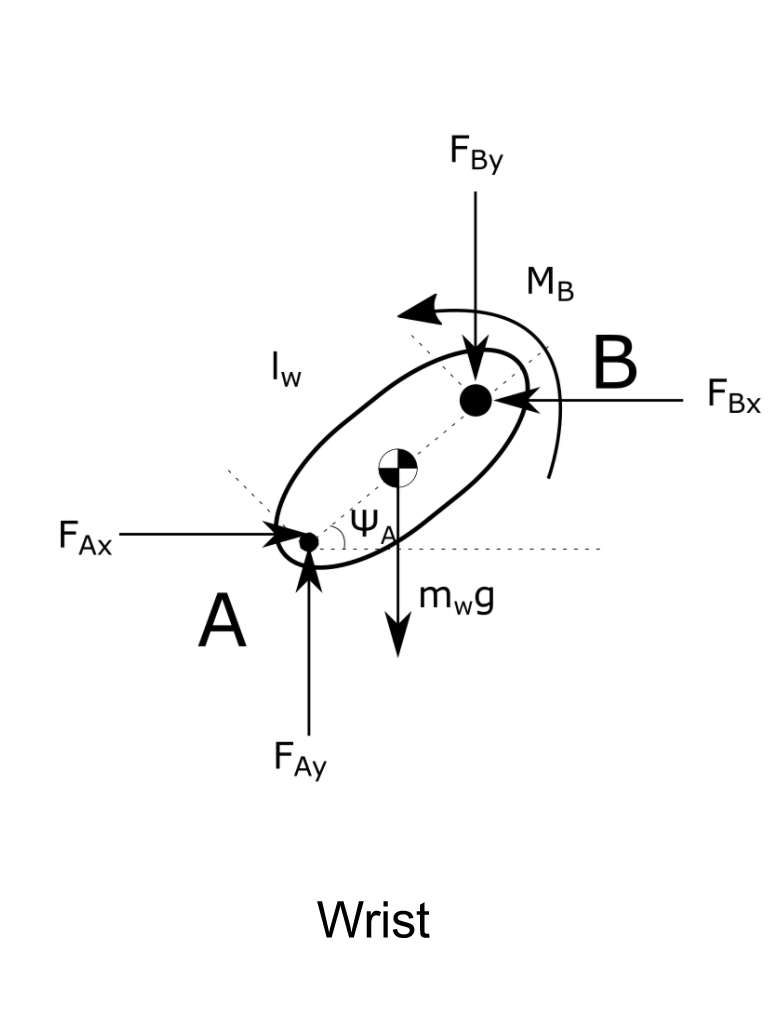
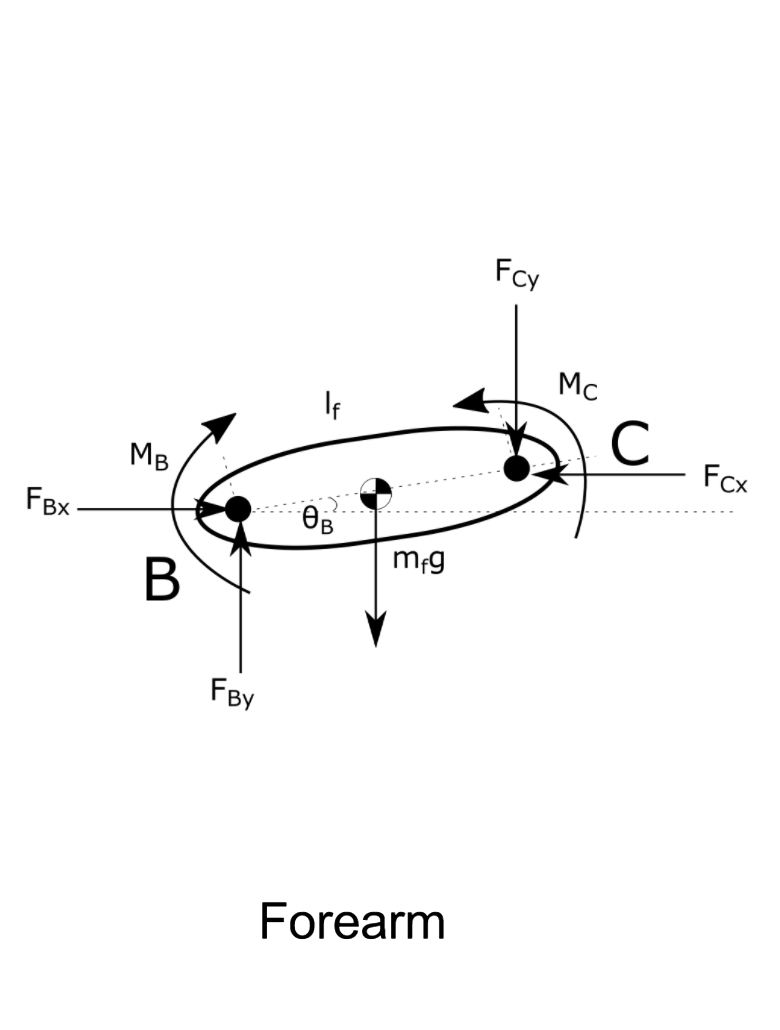
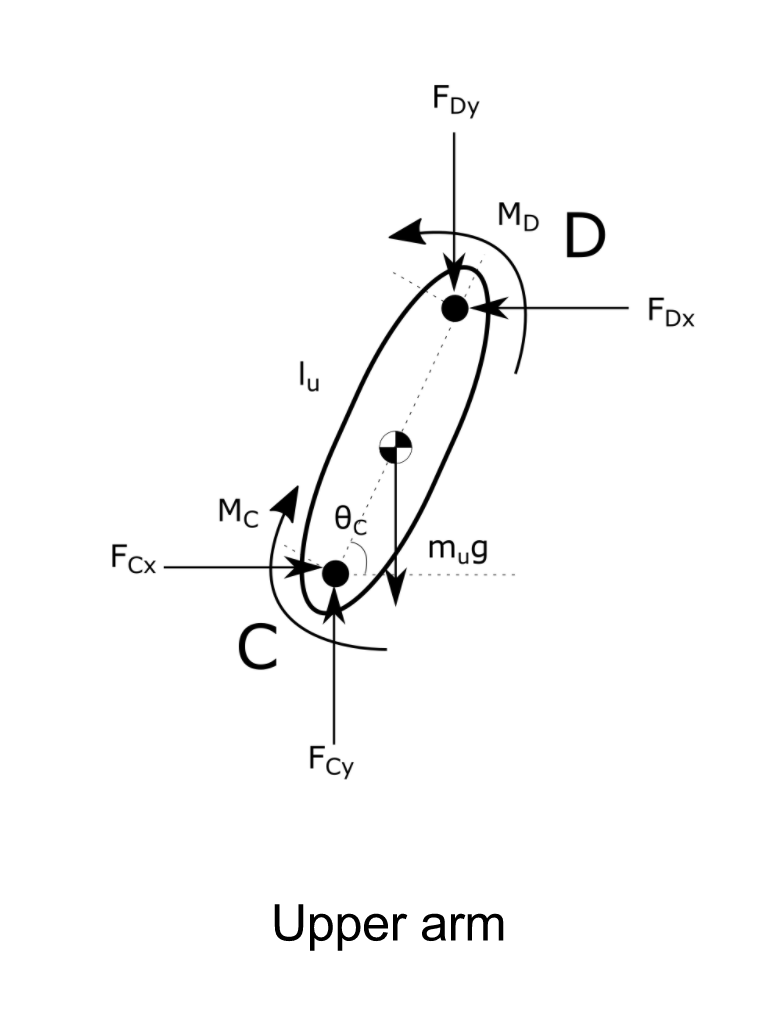
Sum of the forces and sum of the moments calculations on each segment yielded the equations below.

Where F_x are the forces in the x-direction, F_y are the forces in the y-direction and M_B , M_C , M_D are respectivly the moments around B , C, and D. F_Ax , F_Bx , F_Cx , F_Dx are the horizontal forces at each joint, F_Ay , F_By , F_Cy , F_Dy are the vertical forces at each joint, l_w is the length of the wrist, l_f is the length of the forearm, l_u is the length of the upper arm, m_w is the mass of the upper arm, g is the acceleration due to gravity, Φ_A is the angle between the wrist and the horizontal, Θ_B is the angle between the forearm and the horizontal, and Θ_C is the angle between the upper arm and the horizontal axis.

Geometric constraints were imposed on the system to ensure that the lengths of the linked segments did not exceed a user’s vertical and horizontal distance from the piano.

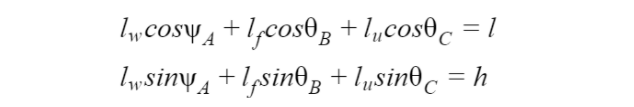
The objective function below was formulated using the equations above where A is a matrix of weighted coefficients to scale the importance of each calculated moment on the pianist’s safety. The inputs are the lengths and masses of the pianist’s limbs, as well as the pianist’s vertical and horizontal distance to the piano (h and l respectively). Outputs are the optimized angles Φ_A , Θ_B , and Θ_C

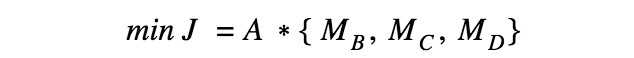
The physical limitations of the body introduce maximum safe possible ranges of motion for the wrist, elbow, and shoulder of the pianist while playing the piano. These ranges serve as upper and lower bounds for the objective function. The ranges are illustrated under the figure below.

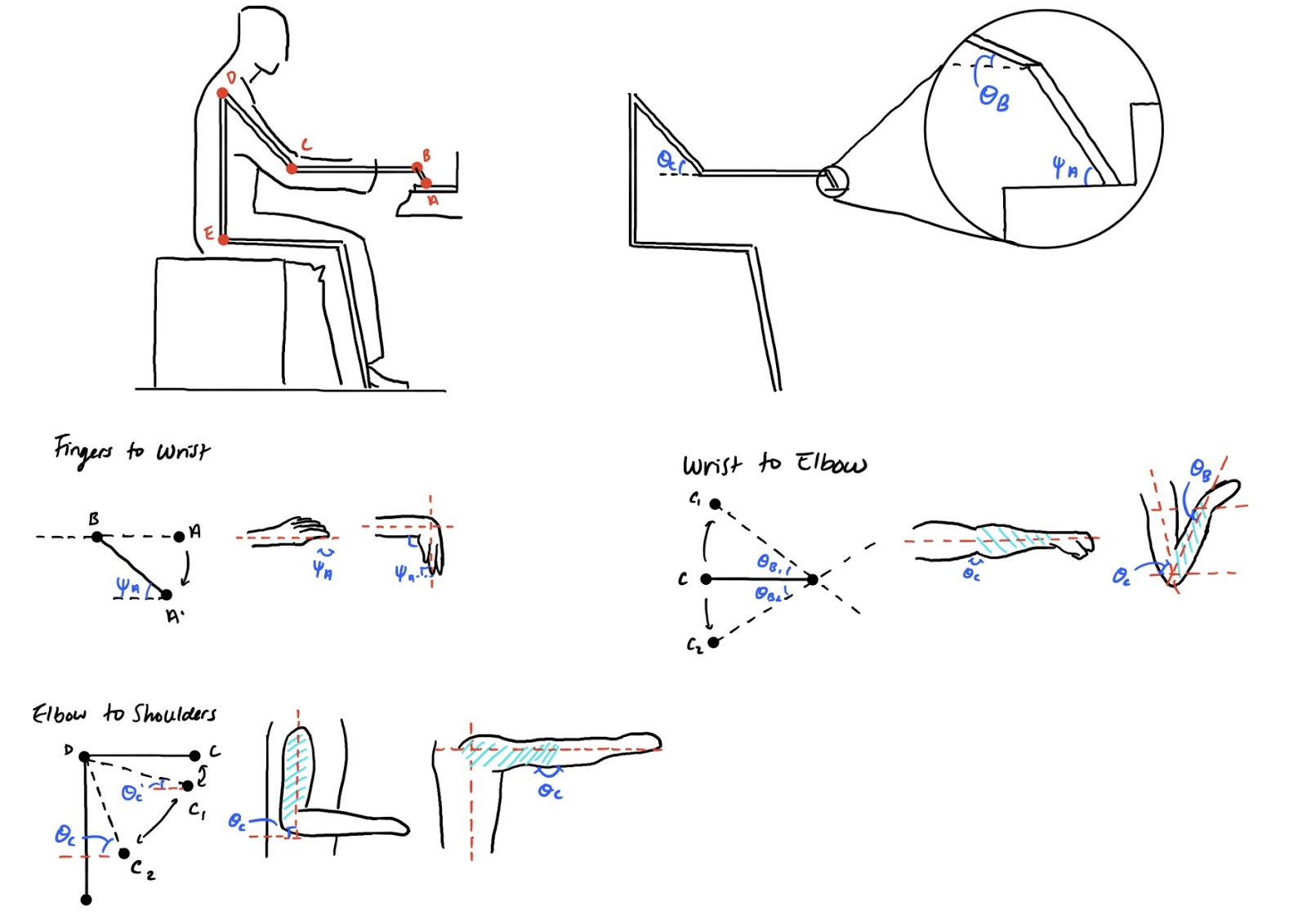
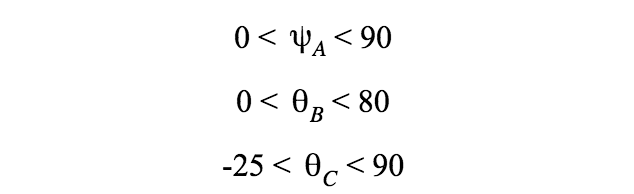
The objective function subject to above constraints were optimized using fmincon as part of the MATLAB optimization toolkit, yielding the optimized posture parameters for the second half of the mathematical model. Sensitivity analyses and simulations are detailed later in this section.

Deviance, Stop, and Rest

The second half of the mathematical model dealt with monitoring the pianist to determine how far the pianist’s posture deviated from the previously calculated optimum position. The deviance from proper form was calculated using the deviance function below.

Where B is a matrix of weighted coefficients to scale the importance of each calculated moment on the pianist’s safety. The square of the difference between the measured and optimal angles is taken to punish large posture deviances and to mitigate the impact of negative numbers on the deviance function.

Research revealed that pianists must rest regularly during long practice sessions to minimize potential strain injuries. To serve this purpose, a summation function was implemented. The function increments by 1 point every second. When the function reaches a threshold specified by an instructor, a flag is thrown and the pianist is instructed to take a rest. When a pianist plays with poor posture, their likelihood of developing a strain injury increases. Thus, when a pianist plays with poor posture, rests should be taken more frequently. To serve this purpose, the summation function was designed to also sum the value of the deviance function every second. This way, a pianist would need to take rests more frequently if they were playing with poor posture. The summation rest function is shown below.

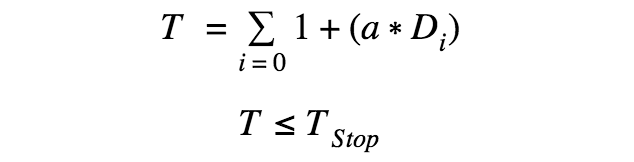
Where T is the current value of the summation function, i is incremented every second, D_i is the deviance function value for the interval, α is a constant to modify the weight of the deviance function, and T_stop is the stopping threshold.

Despite regular rest sessions, it was found that pianists should not play indefinitely. Thus, a stopping function was implemented. The stopping function was a secondary counter to count the number of times a pianist took a break as a result of the rest threshold. When the stopping counter hits the maximum daily allowance set by the piano teacher, the pianist is prompted to stop playing.

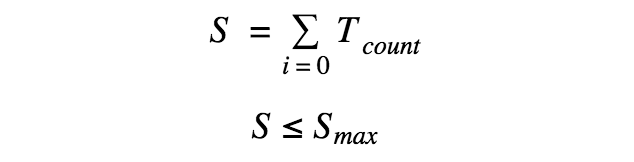
Where T_count is incremented by one every time T_stop from before is exceeded, and S_max is the maximum daily allowance of rests set by the piano teacher.

Sensitivity Analysis

A sensitivity analysis was conducted on the mathematical model using MATLAB. Two main simulations were conducted. In the first simulation, multistart was used to see if the system would resolve to multiple local minima. Multistart operates by repeatedly running local solvers, fmincon for this application, at starting points close to the overall system starting point x0. In this instance, x0 was defined as the starting posture of an average pianist.

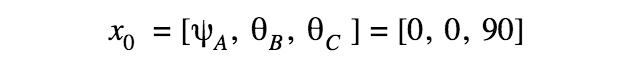
The system failed to converge to a local minima with any of the 20 local solvers. The local solvers either exceeded the iteration limit or the function evaluation limit before converging to any minima. Further investigation revealed that the matrix representing the linear inequality constraints for the objective function was singular. Though the other matrices in the system had relatively low condition numbers, it is likely that this singular matrix rendered the overall problem ill-conditioned.

For the second simulation, the constraints of the mathematical model were modified to investigate the degree of impact of those changes on the optimized posture. Specifically, the weights and lengths of each arm segment were tested for the 5th and 95th percentile body types for males and females. Across these tests, the optimized posture angles differed by at most 6 degrees. Modifying the distance of the pianist to the piano resulted in the largest changes.

Usability Analysis

The designed solution adheres to principles of human factors and general usability. A mobile phone application was chosen to display feedback from the second half of the mathematical model. This decision was made to give the user flexibility in terms of where they wanted their playing feedback to be displayed. The decision helped make the overall solution lightweight, allowing the computational modules that perform the body tracking and analysis to be separated from the display modules. Care was taken to ensure that the mobile interface too adhered to human factors principles. The mobile pane was split into three equal windows. An image of an arm was superimposed on top of the panes to indicate to the user which pane corresponded to which portion of the arm. Colourblind-friendly high contrast colors indicated to the user whether or not arm segments were in the optimal playing position.

The user interface on the computational module was designed with visibility, feedback, and mapping in mind. A live on-screen skeleton superimposed on a video of the playing user was chosen to show the user their current playing position. An ideal skeleton drawing was added to the video, to indicate to the user their goal position. Angles between each body segment and the horizontal were added to the interface to provide further information and assist the user in debugging. Lastly, the user interfaces was designed to include a number of user-entered variables, allowing piano teachers to have full control over rest thresholds, stopping thresholds, body dimensions, and ideal angles.

Designed Prototype

The design of the final prototype consisted of the Kinect technology programmed in Visual Studio, and a web server for live feedback. A user playing the piano interacts with the prototype through two main interfaces, one on a computer, and one on a mobile phone. The computer interface allows the user to enter their optimized posture parameters (from the MATLAB optimization) and body dimensions. The git repository can be found here.

Once the parameters have been entered, a user can elect to start the practice phase, triggering the Kinect motion capture code to execute. A fullscreen live video of the pianist playing is shown (Figure 10). Two skeletons are drawn on this live video in real time. The first ‘seen’ skeleton is what the Kinect detects as the user’s arm. The second skeleton is the ‘ideal’ skeleton, derived from the optimal parameters entered previously, superimposed on top of the screen so that the pianist has an idea of how to correct their posture. Once the screen is activated, a timer begins counting in one second increments. Once the timer reaches the threshold discussed in preceding sections, the pianist is prompted to take a break.

Once the pianist is finished practicing, they can return to the main screen where they can access the history pane. On the history pane, a user can find a video of their preceding practice sessions. The videos contain the ‘seen’ and ‘ideal’ skeletons from the live video feed, allowing a pianist to review their performance after a practice session is over.